The Falling Droplet
We all have seen the rain drops falling on roof tops or road or car roofs, or water droplets falling from tap. When we usually see these phenomenons occur around us they happen within no time. We don’t even notice them. But if we look closely there are very complex physics involved in them. What if we could really slow down time and observe closely these phenomenon occurring? Like this video from Discovery Channel which shows a slow motion capture of a droplet falling into a liquid surface.

After watching below video it really feels like a complex phenomenon doesn’t it? Well indeed it is, and a droplet falling into a liquid surface has been a much researched topic for long time. Experimental and theoretical studies have been going on in this area and this little phenomenon finds large number of application in industry as well. So let us see in this blog where does this ‘falling droplet’ find its place!!
http://www.youtube.com/watch?v=mIB-s5kDdIA
Physics behind ‘the falling droplet’ :
The phenomenon of a liquid droplet interacting with a surface is dependent on many factors. Some of them are properties of droplet, the surface upon which impact takes place, velocity at impact, geometry, as well as the medium through which the droplet travels before impacting the liquid surface. The complexity of detailed fluid mechanics related to liquid droplet and liquid surface interaction continues to be a topic of intensive research, but here in this blog we will try to summarize the process in order to generate curiosity as well as to see how CFD is playing a role in studying this phenomenon.
Depending upon various factors different scenarios exists when a liquid droplet impacts on the liquid surface, i.e. there can be droplet floating or a droplet bounce, also as shown in the video below.
http://www.youtube.com/watch?v=MIFEQ8fNmxE
Coalesce happens as shown in the figure below :

Droplet coalescence
Droplet impact is crucial phenomenon in many natural and industrial processes. For example, impact of raindrops is responsible for aeration of lake which plays important role in sustenance of underwater life. Industrial examples where droplet impact plays important role are fuel injection inside IC engine, spray cooling of turbine blades, surface cooling, inkjet printing etc. Considerable recent attention has been given to drop impact on super hydrophobic surfaces.
Droplet impact in a liquid pool :
When a liquid droplet impacts another liquid body, either liquid pool or drop or film, it can coalesce or bounce, i.e. may remain in one piece or split into several droplets. When a drop impacts on liquid pool, as the drop approaches near liquid surface air is expelled from subsequent air layer. The droplet will bounce or coalesce according to whether this layer achieves critical thickness during impact. In general this critical thickness depends on both fluid properties and system cleanliness. This critical thickness is typically of the order of few micrometers.
Droplet coalescence :
If sub-micrometric thickness is reached, the air layer ruptures in response to cohesive Van Der Waals forces acting between the liquids. Then the large curvature of interface causes the air film between drop and pool retracts quickly and prompting drop coalescence.
Droplet bouncing :
To let the drop bounce, air layer should sustain which exerts a lubrication force and so causes the drop to deform, de-accelerate, and ultimately reverse direction. In other words for the drop to bounce back momentum should be reversed in a finite time by restoring force as in spring. The translational kinetic energy is converted into deformational potential energy associated with surface tension for liquids. This energy is then partly restored to translational motion following impact. Remaining energy is fed into internal drop motion, including waves and oscillations. Droplet bouncing is not stable, we can make it stable by refreshing the air layer under liquid droplet. This air layer can be refreshed by vibrating the water surface.
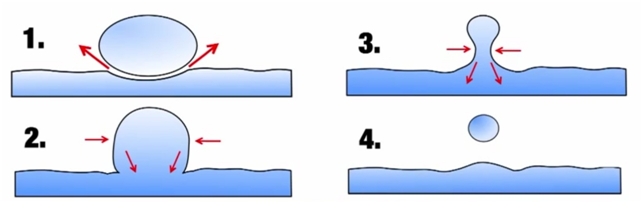
Droplet bouncing
Experiments on ‘The falling droplet’ :
Let us now review an experimental study done on falling droplet. For this we are briefly going to see highlights of the experiment published in "An experimental study of a water droplet impinging on a liquid surface" by S. L. Manzello, J. C. Yang. In this publication an experimental study is presented for water droplet impingement on a liquid surface. The impaction process was recorded using a high-speed digital camera at 1,000 frames/s. The initial droplet diameter was fixed at 3.1 mm ± 0.1 mm, and all experiments were performed in atmospheric air. The impact velocity was varied from 0.36 m/s to 2.2 m/s thus varying the impact Weber number from 5.5 to 206. The impacted liquid surface consisted of two fluids, namely water and methoxy-nonafluorobutane. Here we will see results of water only and for detailed review you can refer to the full paper.
In this experiment the authors have named impacts based on observed results.
Splashes - The impacts which formation of jets
Coalescing - drops causing formation of vortex
The impact is characterised by impact Weber number. The impact Weber number in this study was defined as:
{tex} \rho U^2 D/ \sigma {/tex};
where {tex} D {/tex} is the droplet diameter, {tex} U {/tex} is the impact velocity, {tex} \rho {/tex} is the droplet liquid density, and {tex} \sigma {/tex} is the droplet liquid surface tension.
Figure below displays the time-elapsed images of water droplet impingement upon a 2-mm film of water with an impact Weber number of 206. At a time of 6 ms after impact, the splash created by the water droplet in the 2-mm water layer which resembles the classical crown shape. At 20 ms after impact, the collision dynamics have ended in the water pool. The next sequence considered is water droplets with impact Weber number of 206 into a pool of 7-mm depth, also shown. Water droplet impact into the water pool results in a splash with a jet (defined here as the column of liquid rising from the liquid surface) breaking up at a time of 55 ms after impact.

Now we will see the time-elapsed images for an increase in the pool depth to 10 mm and 25 mm for We number 206. At 25 mm, impact with the water pool forms a jet that is seen to break up at 35 ms after impact. Similar to the 10-mm depth, droplets generated from the liquid jet float upon the liquid surface after returning to the surface.

Now let us see the effect of change in {tex} We {/tex} number. Reduction in {tex} We {/tex} number to 123 means a reduction in impact velocity. For water–water impact, the formation of droplets emanating from the top of the crown does not occur in this case like for {tex} We {/tex} number 206.

Many more experimental studies and results have been published in this paper which is definitely worth a detailed further reading.
Simulation of ‘The falling droplet’ :
The phenomenon of droplet surface interaction has been extensively studied in the simulation world. CFD comes into forefront when we talk about simulating droplet and liquid surface interaction. When we talk about droplet modeling; the extensively used modeling technique for flow modeling is the multiphase model. Application of multiphase models has made it possible to model not only single droplet simulation but also complex droplet dominated flow within spray modelling and microfluidics domain.
|
{modal index.php/en/?option=com_content&view=article&id=129}
 {/modal} {/modal}
{modal index.php/en/?option=com_content&view=article&id=129}
 {/modal} {/modal} |
Let us review how the phenomenon of droplet falling and impact can be simulated using CFD. When we consider a liquid droplet falling through air and impacting another liquid or same liquid surface, the physics involve modelling of multiple phases. For such simulations multiphase models within commercial CFD software like STAR-CCM+ or ANSYS FLUENT can be used. When we are dealing with free surfaces and different phase velocities like in this impact problem, the VOF multiphase model becomes the ideal choice.
The VOF model :
The VOF multiphase model can model two or more immiscible fluids by solving a single set of momentum equations and tracking the volume fraction of each of the fluids throughout the domain. Typical applications of this model are prediction of jet breakup, the motion of large bubbles in a liquid, the motion of liquid after a dam break, and the steady or transient tracking of any liquid-gas interface. In the VOF model within the computational domain under consideration, a particular fluid phase is defined by the volume fraction {tex} q {/tex} in a control volume as the fraction of the {tex} q^{th} {/tex} phase inside a cell. If {tex} q {/tex} is 0 the cell is empty of {tex} q^{th} {/tex} phase and if {tex} q {/tex} is 1 the cell is full of {tex} q^{th} {/tex} phase. If {tex} q {/tex} has any value between 0 and 1 the cell contains the interface between the qth phase and the other phase or phases. Depending upon local values of volume fraction, a single set of Navier–Stokes equations is solved for the computational domain. Also depending upon these volume fraction values, the flow variables and the fluid properties in any given cell are either purely representative of one of the phases, or representative of a mixture of concerned phases. Based on the local value of {tex} q {/tex}, the appropriate fluid properties and flow variables are assigned to each control volume within the domain. In the VOF model, the motion of a moving interface is computed by solving an advection equation for the volume fraction of the {tex} q^{th} {/tex} phase.
Simulation approach :
When considering liquid impact, usually the liquid is assumed to be incompressible. The properties like viscosity and surface tension can be taken as constant. The flow depending upon impacting media and velocity, can be laminar and most of the times Newtonian. There can be possibility of formation of instability at the impact rim but if that is neglected in the simulation we can use a modelling simplification of 2D axis symmetric grid. The simulation has to be carried out using unsteady solver and the VOF model. The simulation time steps used have to be proportional to the impact time scale.
Applications of such droplet CFD simulations :
Such type of droplet impact CFD simulations find wide applications in below areas of science.
- Coating
- Welding
- Microfluidics
- Film drainage in emulsions and foams
- Drying of semi-conductor wafers
‘The falling droplet’ in Industry :
Practical applications of a droplet colliding with a surface include spray cooling of turbine blades, electronic devices, and internal combustion engines. Droplet surface interaction is also important in agriculture, atmospheric sciences, criminal forensics, and fire suppression by sprinkler systems.
http://www.youtube.com/watch?v=aJVVXOMAolQ
http://www.youtube.com/watch?v=qt0lZcL_ZgE
Art in ‘The falling droplet’ :
And now before we end let us also see another aspect of this wonderful physics phenomenon. A falling droplet, as complicated and difficult the physics involved is makes a beautiful and visually pleasing art as well!! Artists like Corrie White have made beautiful photographic art forms out of this simple phenomenon. Some of her sample photographs are below :

Beautiful snap of falling droplet
So to summarize this ‘simple’ phenomenon that we see in daily life of a droplet falling is much more that just ‘simple’. It involves complex physics which can be an interesting research topic. When we talk about CFD simulation this is among the most interesting and detailed multiphase simulation problem and if you come from arts background this is a beautiful art form as well !!
References and sources :
- Physicscentral
- http://www.cd-adapco.com/
- Discovery channel
- ESI group
- An experimental study of a water droplet impinging on a liquid surface S. L. Manzello, J. C. Yang
- www.ansys.com
- Ansys Fluent Users Guide
- Water drop impact into deep pool: Influence of the liquid pool temperature; Stephanie Fest-Santini1,C, Manfredo Guilizzoni2, Maurizio Santini1, Gianpietro Elvio Cossali
- CFD modelling of impact and spreading of droplets on a smooth surface; M. Garbero, M. Vanni and G. Baldi
- Numerical simulations of drop impact and spreading on horizontal andinclined surfaces Siddhartha F. Lunkad, Vivek V. Buwa * , K.D.P. Nigam
- Youtube
- www.cfd-online.com
- Corrie White's website
The Author
{module [317]}